§6 Unsupervised Learning

The Goals of Unsupervised Learning

• The goal is to discover interesting things about the measurements: is there an informative way to visualize the data? Can we discover subgroups among the variables or among the observations?
• We discuss two methods:
  • principal components analysis, a tool used for data visualization or data pre-processing before supervised techniques are applied, and
  • clustering, a broad class of methods for discovering unknown subgroups in data.

Another advantage

• It is often easier to obtain unlabeled data - from a lab instrument or a computer - than labeled data, which can require human intervention.

Principal Components Analysis

• PCA produces a low-dimensional representation of a dataset. It finds a sequence of linear combinations of the variables that have maximal variance, and are mutually uncorrelated.

• Apart from producing derived variables for use in supervised learning problems, PCA also serves as a tool for data visualization.

• The first principal component of a set of features $X_{1}, X_{2}, \ldots, X_{p}$ is the normalized linear combination of the features

  $$Z_{1}=\phi_{11} X_{1}+\phi_{21} X_{2}+\ldots+\phi_{p 1} X_{p}$$

  that has the largest variance. By normalized, we mean that $\sum_{j=1}^{p} \phi_{j 1}^{2}=1$.

• We refer to the elements $\phi_{11}, \ldots, \phi_{p 1}$ as the loadings of the first principal component; together, the loadings make up the principal component loading vector, $\phi_{1}=\left(\begin{array}{llll}\phi_{11} & \phi_{21} & \ldots & \phi_{p 1}\end{array}\right)^{T}$.

• We constrain the loadings so that their sum of squares is equal to one, since otherwise setting these elements to be arbitrarily large in absolute value could result in an arbitrarily large variance.

Computation of Principal Components

• Suppose we have a $n \times p$ data set $\mathbf{X}$. Since we are only interested in variance, we assume that each of the variables in $\mathbf{X}$ has been centered to have mean zero (that is, the column means of $\mathbf{X}$ are zero).

• We then look for the linear combination of the sample feature values of the form

  $$z_{i 1}=\phi_{11} x_{i 1}+\phi_{21} x_{i 2}+\ldots+\phi_{p 1} x_{i p}$$

  for $i=1, \ldots, n$ that has largest sample variance, subject to the constraint that $\sum_{j=1}^{p} \phi_{j 1}^{2}=1$.

• Since each of the $x_{i j}$ has mean zero, then so does $z_{i 1}$ (for any values of $\phi_{j 1}$ ). Hence the sample variance of the $z_{i 1}$ can be written as $\frac{1}{n} \sum_{i=1}^{n} z_{i 1}^{2}$.

• Plugging in the first principal component loading vector solves the optimization problem

  $$\underset{\phi_{11}, \ldots, \phi_{p 1}}{\operatorname{maximize}} \frac{1}{n} \sum_{i=1}^{n}\left(\sum_{j=1}^{p} \phi_{j 1} x_{i j}\right)^{2} \text{ subject to } \sum_{j=1}^{p} \phi_{j 1}^{2}=1$$

• This problem can be solved via a singular-value decomposition of the matrix $\mathbf{X}$ , a standard technique in linear algebra.

• We refer to $Z_{1}$ as the first principal component, with realized values $z_{11}, \ldots, z_{n 1}$.

Geometry of PCA

• The loading vector $\phi_{1}$ with elements $\phi_{11}, \phi_{21}, \ldots, \phi_{p 1}$ defines a direction in feature space along which the data vary the most.
• If we project the $n$ data points $x_{1}, \ldots, x_{n}$ onto this direction, the projected values are the principal component scores $z_{11}, \ldots, z_{n 1}$ themselves.

Further principal components

• The second principal component is the linear combination of $X_{1}, \ldots, X_{p}$ that has maximal variance among all linear combinations that are uncorrelated with $Z_{1}$.

• The second principal component scores $z_{12}, z_{22}, \ldots, z_{n 2}$ take the form

  $$z_{i 2}=\phi_{12} x_{i 1}+\phi_{22} x_{i 2}+\ldots+\phi_{p 2} x_{i p}$$

  where $\phi_{2}$ is the second principal component loading vector, with elements $\phi_{12}, \phi_{22}, \ldots, \phi_{p 2}$.

• It turns out that constraining $Z_{2}$ to be uncorrelated with $Z_{1}$ is equivalent to constraining the direction $\phi_{2}$ to be orthogonal (perpendicular) to the direction $\phi_{1}.$ And so on.

• The principal component directions $\phi_{1}, \phi_{2}, \phi_{3}, \ldots$ are the ordered sequence of right singular vectors of the matrix $\mathbf{X}$ , and the variances of the components are $\frac{1}{n}$ times the squares of the singular values. There are at most $\min (n-1, p)$ principal components.

PCA find the hyperplane closest to the observations

• The first principal component loading vector has a very special property: it defines the line in $p$-dimensional space that is closest to the $n$ observations (using average squared Euclidean distance as a measure of closeness)
• The notion of principal components as the dimensions that are closest to the $n$ observations extends beyond just the first principal component.
• For instance, the first two principal components of a data set span the plane that is closest to the $n$ observations, in terms of average squared Euclidean distance.

Scaling of the variables matters

• If the variables are in different units, scaling each to have standard deviation equal to one is recommended.
• If they are in the same units, you might or might not scale the variables.

Proportion Variance Explained

• To understand the strength of each component, we are interested in knowing the proportion of variance explained (PVE) by each one.

• The total variance present in a data set (assuming that the variables have been centered to have mean zero) is defined as

  $$\sum_{j=1}^{p} \operatorname{Var}\left(X_{j}\right)=\sum_{j=1}^{p} \frac{1}{n} \sum_{i=1}^{n} x_{i j}^{2}$$

  and the variance explained by the $m$ th principal component is

  $$\operatorname{Var}\left(Z_{m}\right)=\frac{1}{n} \sum_{i=1}^{n} z_{i m}^{2}$$

• It can be shown that $\sum_{j=1}^{p} \operatorname{Var}\left(X_{j}\right)=\sum_{m=1}^{M} \operatorname{Var}\left(Z_{m}\right)$ , with $M=\min (n-1, p)$.

• Therefore, the PVE of the $m$ th principal component is given by the positive quantity between 0 and 1

  $$\frac{\sum_{i=1}^{n} z_{i m}^{2}}{\sum_{j=1}^{p} \sum_{i=1}^{n} x_{i j}^{2}}$$

How many principal components should we use?

If we use principal components as a summary of our data, how many components are sufficient?

• No simple answer to this question, as cross-validation is not available for this purpose.
  • Why not?
  • When could we use cross-validation to select the number of components?
• the “scree plot” on the previous slide can be used as a guide: we look for an “elbow”

Clustering

• Clustering refers to a very broad set of techniques for finding subgroups, or clusters, in a data set.
• We seek a partition of the data into distinct groups so that the observations within each group are quite similar to each other,
• It make this concrete, we must define what it means for two or more observations to be similar or different.
• Indeed, this is often a domain-specific consideration that must be made based on knowledge of the data being studied.

PCA vs Clustering

• PCA looks for a low-dimensional representation of the observations that explains a good fraction of the variance.
• Clustering looks for homogeneous subgroups among the observations.

Two clustering methods

• In $**K$ -means clustering**, we seek to partition the observations into a pre-specified number of clusters,
• In hierarchical clustering, we do not know in advance how many clusters we want; in fact, we end up with a tree-like visual representation of the observations, called a dendrogram, that allows us to view at once the clusterings obtained for each possible number of clusters, from $1$ to $n$.

$K$-means clustering

• Let $C_{1}, \ldots, C_{K}$ denote sets containing the indices of the observations in each cluster. These sets satisfy two properties:

  1. $C_{1} \cup C_{2} \cup \ldots \cup C_{K}=\{1, \ldots, n\}.$ In other words, each observation belongs to at least one of the $K$ clusters.
  2. $C_{k} \cap C_{k^{\prime}}=\emptyset$ for all $k \neq k^{\prime}$. In other words, the clusters are non-overlapping: no observation belongs to more than one cluster.

  For instance, if the $i$ th observation is in the $k$ th cluster, then $i \in C_{k}$.

• The idea behind $K$ -means clustering is that a good clustering is one for which the within-cluster variation is as small as possible.

• The within-cluster variation for cluster $C_{k}$ is a measure $\mathrm{WCV}\left(C_{k}\right)$ of the amount by which the observations within a cluster differ from each other.

• Hence we want to solve the problem

  $$\operatorname{minimize}_{C_{1}, \ldots, C_{K}}\left\{\sum_{k=1}^{K} \mathrm{WCV}\left(C_{k}\right)\right\}$$

• In words, this formula says that we want to partition the observations into $K$ clusters such that the total within-cluster variation, summed over all $K$ clusters, is as small as possible.

How to define within-cluster variation?

• Typically we use Euclidean distance

  $$\mathrm{WCV}\left(C_{k}\right)=\frac{1}{\left|C_{k}\right|} \sum_{i, i^{\prime} \in C_{k}} \sum_{j=1}^{p}\left(x_{i j}-x_{i^{\prime} j}\right)^{2}$$

  where $\left|C_{k}\right|$ denotes the number of observations in the $k$ th cluster.

• The optimization problem that defines $K$ -means clustering,

  $$\underset{C_{1}, \ldots, C_{K}}{\operatorname{minimize}}\left\{\sum_{k=1}^{K} \frac{1}{\left|C_{k}\right|} \sum_{i, i^{\prime} \in C_{k}} \sum_{j=1}^{p}\left(x_{i j}-x_{i^{\prime} j}\right)^{2}\right\}$$

$K$-Means Clustering Algorithm

1. Randomly assign a number, from $1$ to $K$ , to each of the observations. These serve as initial cluster assignments for the observations.
2. Iterate until the cluster assignments stop changing:
   1. For each of the $K$ clusters, compute the cluster centroid. The $k$ th cluster centroid is the vector of the $p$ feature means for the observations in the $k$ th cluster.
   2. Assign each observation to the cluster whose centroid is closest (where closest is defined using Euclidean distance).

Properties of the Algorithm

• This algorithm is guaranteed to decrease the value of the objective at each step. Note that

  $$\frac{1}{\left|C_{k}\right|} \sum_{i, i^{\prime} \in C_{k}} \sum_{j=1}^{p}\left(x_{i j}-x_{i^{\prime} j}\right)^{2}=2 \sum_{i \in C_{k}} \sum_{j=1}^{p}\left(x_{i j}-\bar{x}_{k j}\right)^{2}$$

  where $*\bar{x}_{k j}=\frac{1}{\left|C_{k}\right|} \sum_{i \in C_{k}} x_{i j}*$ is the mean for feature $j$ in cluster $C_{k}$.

• however it is not guaranteed to give the global minimum.

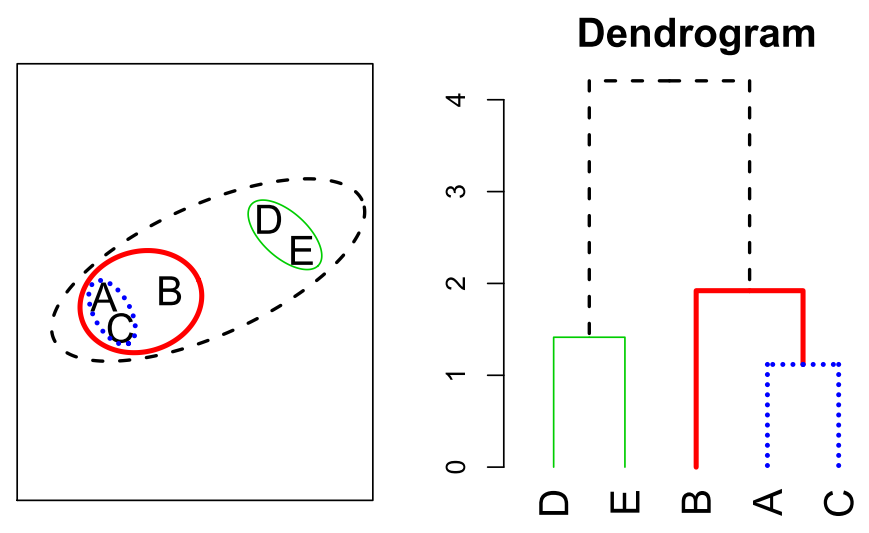
Hierarchical Clustering

• $K$ -means clustering requires us to pre-specify the number of clusters $K$. This can be a disadvantage (later we discuss strategies for choosing $K$ )
• Hierarchical clustering is an alternative approach which does not require that we commit to a particular choice of $K$.
• In this section, we describe bottom-up or agglomerative clustering. This is the most common type of hierarchical clustering, and refers to the fact that a dendrogram is built starting from the leaves and combining clusters up to the trunk.

Hierarchical Clustering Algorithm

The approach in words:

• Start with each point in its own cluster.
• Identify the closest two clusters and merge them,
• Repeat.
• Ends when all points are in a single cluster.

Types of Linkage

• Complete

  Maximal inter-cluster dissimilarity. Compute all pairwise dissimilarities between the observations in cluster A and the observations in cluster B, and record the largest of these dissimilarities.

• Single

  Minimal inter-cluster dissimilarity. Compute all pairwise dissimilarities between the observations in cluster A and the observations in cluster B, and record the smallest of these dissimilarities.

• Average

  Mean inter-cluster dissimilarity. Compute all pairwise dissimilarities between the observations in cluster A and the observations in cluster B, and record the average of these dissimilarities.

• Centroid

  Dissimilarity between the centroid for cluster A (a mean vector of length $p$) and the centroid for cluster B. Centroid linkage can result in undesirable inversions.

Choice of Dissimilarity Measure

• So far have used Euclidean distance.
• An alternative is correlation-based distance which considers two observations to be similar if their features are highly correlated.
• This is an unusual use of correlation, which is normally computed between variables; here it is computed between the observation profiles for each pair of observations.

Practical issues

• Should the observations or features first be standardized in some way? For instance, maybe the variables should be centered to have mean zero and scaled to have standard deviation one.
• In the case of hierarchical clustering,
  • What dissimilarity measure should be used?
  • What type of linkage should be used?
• How many clusters to choose? (in both $K$ -means or hierarchical clustering). Difficult problem. No agreed-upon method.

Conclusions

• Unsupervised learning is important for understanding the variation and grouping structure of a set of unlabeled data, and can be a useful pre-processor for supervised learning
• It is intrinsically more difficult than supervised learning because there is no gold standard (like an outcome variable) and no single objective (like test set accuracy)
  • It is an active field of research, with many recently developed tools such as self-organizing maps, independent components analysis and spectral clustering.

— Jul 15, 2022

§6 Unsupervised Learning by Lu Meng is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Permissions beyond the scope of this license may be available at About.